Linear regression is an amazingly powerful concept in statistical modelling. It forms a major part of lots of first year statistics cources and how to deal with problems with linear regression can form second year units by themselves!
This post goal is to through the use of AFL data provide an intituitive guide to linear regression.
So why use AFL data?
With learning context and motivation are key. I think this is especially true with statistics. Hopefully you have found this blog through a combination of wanting to learn some stats, some R and an interest in footy.
Linear Regression
Lets think about an example we know to be true. Lots of people do fantasy sports be it for fun with mates or having a punt. We know that AFL Fantasy points are linear in nature. But lets pretend for a second that we didn’t know how points were allocated for fantasy.
We are interested in looking at whether the amount of kicks influences the fantsy points and if so by how much?
Step One - Get the data
Our first step would be just to get the data and explore it.
Thankfully there exists an AFL R package so we can go exploring.
library(fitzRoy)
library(tidyverse)## -- Attaching packages -------------------------------- tidyverse 1.2.1 --## v ggplot2 2.2.1 v purrr 0.2.5
## v tibble 1.4.2 v dplyr 0.7.5
## v tidyr 0.8.1 v stringr 1.3.1
## v readr 1.1.1 v forcats 0.3.0## -- Conflicts ----------------------------------- tidyverse_conflicts() --
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()df<-fitzRoy::player_statsStep Two - Plot the data
Step two, in practice I don’t think is done as often as it should be. We can learn lots of things from visually inspecting our data.
df%>%
select(K,AF)%>%
ggplot(aes(x=K,y=AF))+geom_point()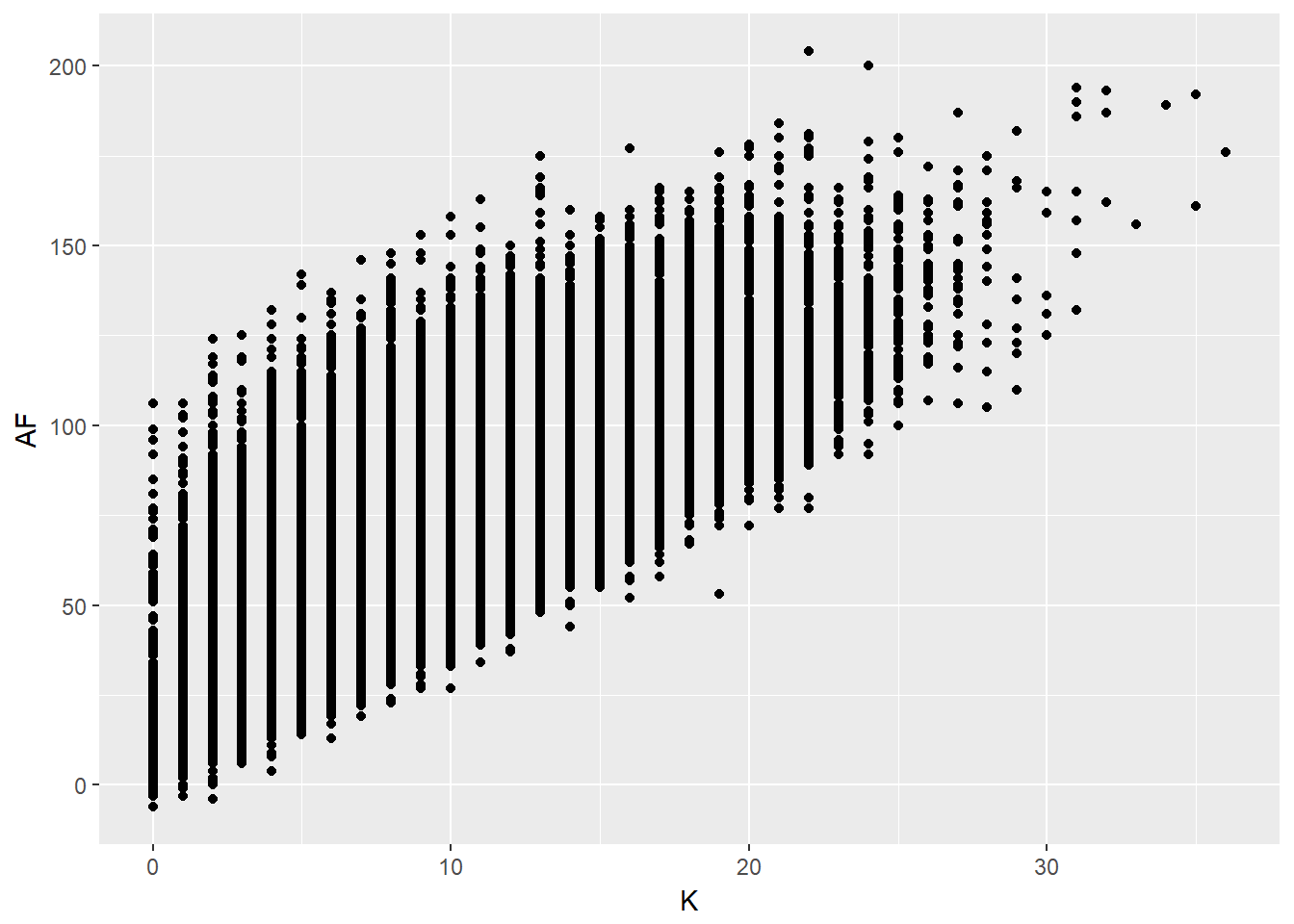 Looking at this it would seem as though on average if a player has more kicks they will get more fantasy points. Intuitively the relationship looks fairly obvious, players who get more kicks get more fantasy points. BUT we might want a more precise estimate of the relationship between kicks and fantasy points. This is where our linear regression comes in handy dandy.
Looking at this it would seem as though on average if a player has more kicks they will get more fantasy points. Intuitively the relationship looks fairly obvious, players who get more kicks get more fantasy points. BUT we might want a more precise estimate of the relationship between kicks and fantasy points. This is where our linear regression comes in handy dandy.
Step Three - The linear regression
The way we have posed this problem is that AF (Fantasy scores) is a function of kicks. We would write this out to begin with as
AF ~ Kicks This reads as AF (our dependant variable as it depends on Kicks) is a function of Kicks (our independant variable).
All models are wrong!
George Box:
All models are wrong but some are useful
Models are by nature a simplifcation of reality, in this case we know that Kicks are not the only variable that has an effect on fantasy scores.
Another quote from George Box which is my personal favourite:
Since all models are wrong the scientist cannot obtain a “correct” one by excessive elaboration. On the contrary following William of Occam he should seek an economical description of natural phenomena. Just as the ability to devise simple but evocative models is the signature of the great scientist so overelaboration and overparameterization is often the mark of mediocrity.
So there you go, all models are wrong, we can’t take into account all the things that might effect our dependant variable. Think about team ratings (we will build a team rating linear regression later) how can you possible take into account all the factors that might affect how good a team is. There has and always will be some natural variable and some uncertainty around our estimates and isn’t that beautiful.
So now we now, that there will always be somethings that we can’t account for and things we could account for but don’t want to be it for model simplicity/interprebility, data issues or a host of other reasons. Hence we update our little equation above all these random and unaccounted for things ϵ , and we write our new equation as AF Kicks+ϵ we can think of ϵ as all the things that effect fantasy scores that are not kicks.
Get me my coefficiants
library(fitzRoy)
library(tidyverse)
df<-fitzRoy::player_stats
eq1<-lm(AF~K, data=df)
summary(eq1)##
## Call:
## lm(formula = AF ~ K, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -63.583 -11.892 -1.789 9.832 91.556
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 26.8231 0.1386 193.5 <2e-16 ***
## K 4.7242 0.0133 355.2 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 16.77 on 76294 degrees of freedom
## Multiple R-squared: 0.6232, Adjusted R-squared: 0.6232
## F-statistic: 1.262e+05 on 1 and 76294 DF, p-value: < 2.2e-16So what is going on here?
First, we load our packages that we need (fitzRoy, tidyverse). Then we get the player_stats data and call it df df<-fitzRoy::player_stats. After that we fit our linear regression which we recall was AF~K we do this using the lm function in R and the dataset we use to fit the model is df from earlier.
Then we use summary(eq1) to see our output and coefficients.
Theres a lot going on there, so lets dig in and find what we are looking for.
Question and Answers
I am going to give something new a go here so I may even have to rewrite this blog post!
You said earlier that a model can’t explain everything but it can explain somethings?
That is true, a model is an abstraction away from reality, and there will always be some unexplained variation that we can’t or choose not to control for. A measure of the variation that our models explains is our Multiple R-squared for this example our Mutliple R-squared:* is 0.6235 you can interpret this by saying that 62.35% of the variation in fantasy scores is accounted for by our model (in this case just kicks)*
In general you want your R2 Multple R-squared to be higher rather than lower. The question of how high depends on what kind of data you are looking at. AFL modelling can be messy and noisy and affected by a whole heap of things outside of the model. But in this specific example because we know that fantasy scores are a direct function of the game statistics we would expect an R2 as close to one as possible if we knew all the variables in the fantasy scores.
What about this significance test and p-values that everyone is crazy for can you please tell me more
That is a great question and you have really opened up a can of worms.
Great so what is a the bloody thing!
From the ASA statment on p-values
Informally, a p-value is the probability under a specified statistical model that a statistical summary of the data (e.g., the sample mean difference between two compared groups) would be equal to or more extreme than its observed value.
So the idea is, we start off with this idea of a null hypothesis which in our example above for the coeffcient for kicks is that nothing is going on, that β1 our coefficient for kicks is equal to 0. This nothing going on here is the same null hypothesis test for all the coefficents that lm would have produced estimates for if we added in more variables like handballs, marks, tackles etc.
So we have our null hypothesis, we assume nothings going on and then we calculate the probability of getting some test statistic as or more extreme to the one observed (4.726). So if nothing was going on here, the probability of getting the value of 4.726 for Kicks is small (<2e-16). So, if the P-value is small, what you’re seeing is the probability of observing a test statistic as extreme as the one seen, is low if the null hypothesis were true (nothing is going on β1=0)
Fantasy scores are just a linear model right?
Something that might be fun to do (well is fun to ) you can actually get how AF calculates the scores. So why not knowing this put in those variables and you should get what the coefficients are right?
library(fitzRoy)
library(tidyverse)
df<-fitzRoy::player_stats
eq1<-lm(AF~K +HB+M +T +FF +FA+HO +G +B, data=df)
summary(eq1)##
## Call:
## lm(formula = AF ~ K + HB + M + T + FF + FA + HO + G + B, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.281e-09 -2.000e-14 3.000e-14 8.000e-14 6.089e-11
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -8.795e-12 8.881e-14 -9.903e+01 <2e-16 ***
## K 3.000e+00 8.542e-15 3.512e+14 <2e-16 ***
## HB 2.000e+00 7.584e-15 2.637e+14 <2e-16 ***
## M 3.000e+00 1.437e-14 2.087e+14 <2e-16 ***
## T 4.000e+00 1.405e-14 2.847e+14 <2e-16 ***
## FF 1.000e+00 3.183e-14 3.141e+13 <2e-16 ***
## FA -3.000e+00 3.098e-14 -9.684e+13 <2e-16 ***
## HO 1.000e+00 4.760e-15 2.101e+14 <2e-16 ***
## G 6.000e+00 3.230e-14 1.857e+14 <2e-16 ***
## B 1.000e+00 4.271e-14 2.341e+13 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8.265e-12 on 76286 degrees of freedom
## Multiple R-squared: 1, Adjusted R-squared: 1
## F-statistic: 9.257e+28 on 9 and 76286 DF, p-value: < 2.2e-16Yep there you go, the intercept is basically 0, Kicks are 3, handballs are 2, marks are 3, tackles are 4 etc. We can also see our R2 is 1
Using Linear regression to build a team rating system
Before you get all angry and don’t @me here me out. Linear regression is a powerful tool and can even form part of a PhD thesis in footy statistics. Its a great building block to build from just as more commonly used ELOS are another great building block and another post.
Using what we learnt above, we might want to formulate our regression so that we can predict the margin of win/loss for the home team.
margin=Home.Score−Away.Score
Now we have margin as our outcome variable we want to try and predict what would be our actual predictors? Well we can’t use the actual Home.Score and Away.Score, thats just silly.
Lets write it out like:
margini=homequalityi−awayqualityi+ϵ
Where for each game we have our home team, our away team and some measure of their quality.
So how do we do this as a regression?
yi=∑xijβj+ϵ
library(tidyverse)
library(fitzRoy)
matches<-fitzRoy::get_match_results()
matches<-matches%>%filter(Season==2017)
teams<-unique(matches$Home.Team)
all.teams <- sort(unique(teams))
y <- with(matches, Home.Points-Away.Points)
X0 <- as_tibble(matrix(0,nrow(matches),length(all.teams)))
names(X0) <- all.teams
for(mtrx in all.teams) {
X0[[mtrx]] <- 1*(matches$Home.Team==mtrx) - 1*(matches$Away.Team==mtrx)
}
X <- X0[,names(X0) != "Carlton"]
linearmodel <- lm(y ~ 0 + ., data=X)
head(coef(summary(linearmodel)))## Estimate Std. Error t value Pr(>|t|)
## Adelaide 48.061201 10.08678 4.7647734 3.747107e-06
## `Brisbane Lions` -9.127578 10.37399 -0.8798521 3.800509e-01
## Collingwood 19.240427 10.38167 1.8533074 6.538887e-02
## Essendon 20.508245 10.06377 2.0378301 4.295321e-02
## Footscray 15.920944 10.39112 1.5321677 1.271444e-01
## Fremantle -4.472357 10.38228 -0.4307685 6.671250e-01linearmodelratings<-as.data.frame(coef(summary(linearmodel)))
linearmodelratings[with(linearmodelratings, order(-Estimate)), ]## Estimate Std. Error t value Pr(>|t|)
## Adelaide 48.061201 10.086776 4.7647734 3.747107e-06
## `Port Adelaide` 38.558691 10.293608 3.7458868 2.382649e-04
## Sydney 36.554207 9.972891 3.6653571 3.204001e-04
## Richmond 35.677314 9.902028 3.6030311 4.015994e-04
## GWS 32.594485 10.096762 3.2282115 1.467452e-03
## Geelong 31.789616 10.095630 3.1488492 1.903952e-03
## Melbourne 22.859720 10.171242 2.2474856 2.575873e-02
## `West Coast` 21.917010 10.210958 2.1464207 3.310749e-02
## Essendon 20.508245 10.063766 2.0378301 4.295321e-02
## Collingwood 19.240427 10.381671 1.8533074 6.538887e-02
## `St Kilda` 17.228341 10.373975 1.6607271 9.841758e-02
## Footscray 15.920944 10.391124 1.5321677 1.271444e-01
## Hawthorn 11.871564 10.381808 1.1434967 2.542711e-01
## `North Melbourne` 4.301616 10.382199 0.4143261 6.791027e-01
## Fremantle -4.472357 10.382276 -0.4307685 6.671250e-01
## `Gold Coast` -7.541466 10.172218 -0.7413788 4.593792e-01
## `Brisbane Lions` -9.127578 10.373991 -0.8798521 3.800509e-01