So it is approaching AFL mens season, which means that soon everyones twitter feed, Facebook and emails will get clogged up with various tipsters. People saying they have won at 60% of the time over last season and therefor you should pay them money and follow their tips!
But how can you assess the accuracy of a tipster? Very few would allow a full interrogation of the model. What this means that you if you decide to follow them are doing so only based on their output, and that could be an issue.
Lets take a simple thought experiment. Lets say we have a biased coin toss and lets put deliberately for this experiment the probability of heads to be 0.55
library(tidyverse)## ── Attaching packages ───────────────────────────────────────────────────────── tidyverse 1.2.1 ──## ✔ ggplot2 3.1.0 ✔ purrr 0.3.0
## ✔ tibble 2.0.1 ✔ dplyr 0.8.0.1
## ✔ tidyr 0.8.3 ✔ stringr 1.4.0
## ✔ readr 1.3.1 ✔ forcats 0.4.0## ── Conflicts ──────────────────────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()flips = 10000
pHeads =0.55
set.seed(10032019)
coinflips = sample( x=c(0,1),prob = c(1-pHeads,pHeads),size=flips,replace=T)
count_heads = cumsum(coinflips)
flips= 1:flips
runProp = count_heads/flips
flip_data <- data.frame(run=1:10000,prop=runProp)
ggplot(flip_data,aes(x=run,y=prop,frame=run)) +
geom_path(aes(cumulative=T))+xlim(1,500)+ylim(0.45,1.0)+
geom_hline(yintercept = 0.58)+ geom_vline(xintercept=80)+
geom_hline(yintercept = 0.55)+
ggtitle("Running Proportion Heads of a biased Coin")+
ylab("Proportion of Heads")+xlab("Flip Number")## Warning: Ignoring unknown aesthetics: cumulative## Warning: Removed 9500 rows containing missing values (geom_path).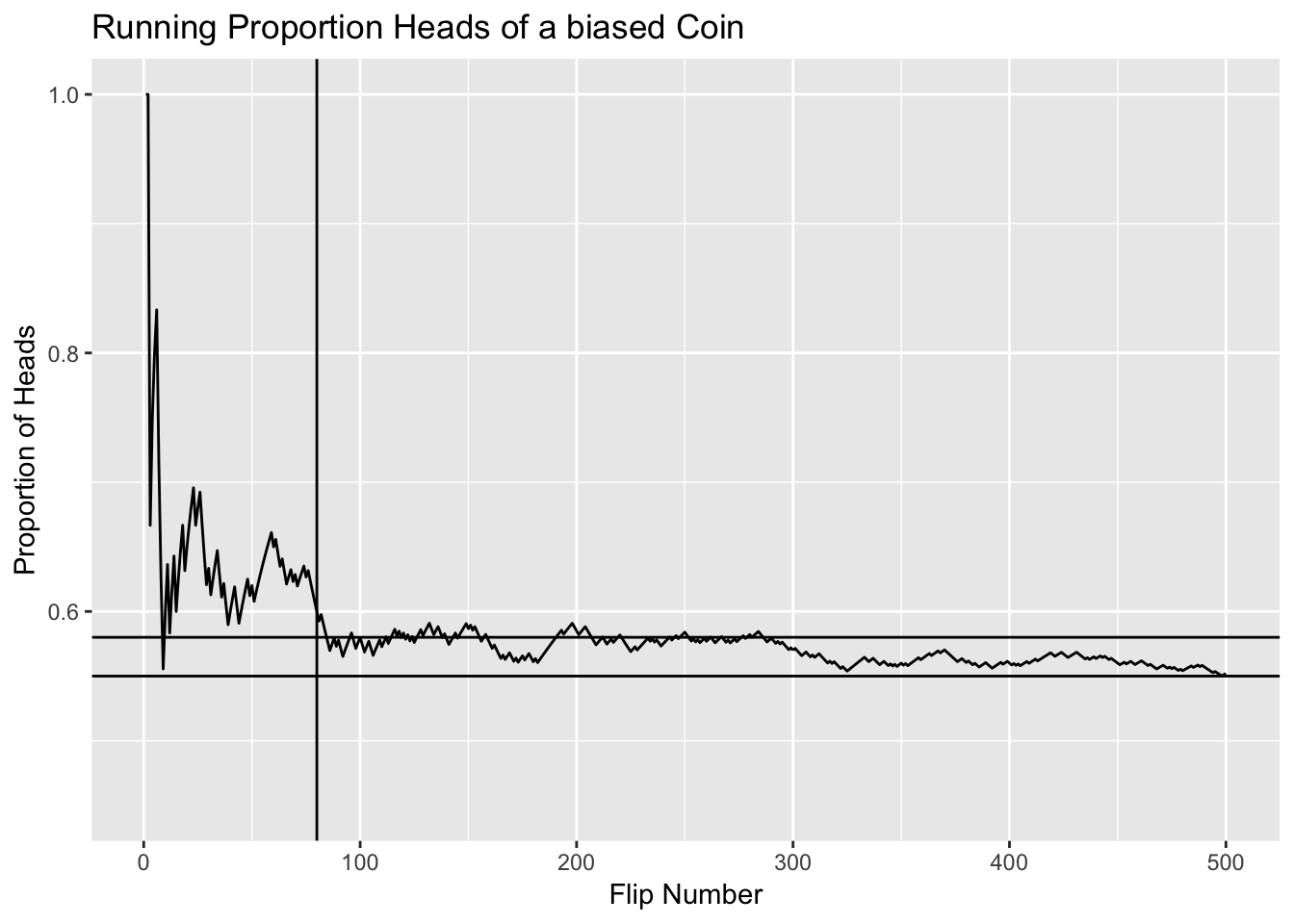
Keep in mind this is a simulation I have put in the odds of a head are 0.55. For reference I added some lines, we can see that our reference line geom_hline(yintercept=0.58) is 0.58, we can see even after 200 bets we are still hovering around 0.58. Of course that’s what a tipster would say, that their win rate is 0.58. But we know thats not true long term from the simulation. The other reference line i have added is geom_vline(xintercept=80) we can see that that performance would look to be even slightly higher (about 0.6) and again, we know that this is a simulation and that long term its 0.55. How long is an AFL season? How many games to you realistically expect people to have bet on in a season?
Another thing to think about with regards to the long term performance that we know. Think about the way averages work. If after 250 bets, the proportion of heads is 0.58, in the next 250 bets what proportion of heads is needed to get the running proportion of heads down to 0.55? Maybe have a think about that next time before you pay for a service.